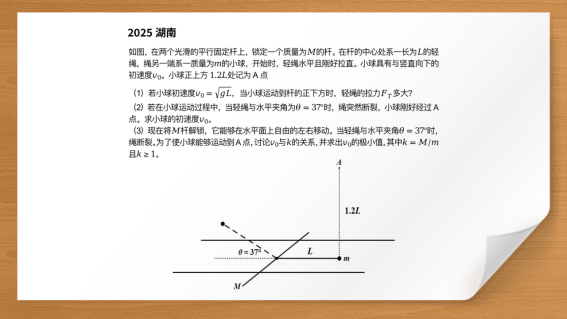这些问题在2025年审查物理学院有多困难？如何使用矢量计算思想解决相对孩子运动的问题与平坦的铸造运动相结合？如何解决带电颗粒的圆形运动和椭圆运动？如何比较和应用开普勒定律来解决移动椭圆的粒子的相关问题？ 6月22日12:00，启动了249阶段的“张乔阳的物理课”。 Sohu的创始人，董事长兼首席执行官Zhang Chaoyang以及物理学博士，离线硬核减少了2025年大学入学的两个最终问题，Hunan Province和四个Northheast Provinces（Heilongjiang，Heilongjiang，Jilin，Jilin，Jilies和Internal Notheria and Mongolia和Internal Mongolia），清楚地表明了与学生保持平整的学生。 2025 Hunan College审查问题（2025 Hunan Physics College入学考试最终问题）此问题被认为是在整齐的轨道上摔断球的​​过程，其中有质量M的杆已连接用不可避免的光线绳到球上，并以稳定的杆M角释放球，使球达到A点A。固定球固定，以初始速度垂直释放球，并以圆形运动移动。当球直接移动到轴的底部时，力的力可以使绳索的绳索减去球的重力等于圆形运动的离心力。扩展全文 在能量的谨慎时，当球直接在轴下时，初始enekinetic的riya被转换为动能和潜在的球能量。 您可以找到绳索拧紧 （2）检查物理过程，球以V0的一定初始速度垂直释放。当它移至轴左上方37°时，打破光线。假设当绳索被破坏时，球的速度为V2。之后，球会抛物线移动，抛物线运动可以到达A点，并且可以从初始速度逆转。该问题的给定角度为37°的特殊角度，可以使用SIN37°= 0.6和COS37°= 0.8来简化计算。 （张乔阳检查物理过程） 寓言运动的水平和垂直方向之间的距离是 具有一些代数技能，将初始速度设置为 用能量节省， v2的当时以及水平和垂直方向 可以在水平方向上获得相等的速度 i输入垂直方向超速移动的同等运动 可以获得V0初始速度 （张Chaoyang计算初始速度） （3）问题（3）与问题（2）相似，但是由于轴可以在水平方向自由移动并固定在垂直方向上，因此找到点A的初始V0速度与轴和球的质量比与球与球的质量比与V0初始速度的最小值之间的关系。 在球的运动中，项目水平方向上绳索上的张力张力的离子通常不是0，因此绳索将导致轴产生水平加速度，并且加速度是可变的。球和轴的运动将更加复杂，但是通过使用能量的照顾并保持动力，您不必考虑每一刻，您只需要考虑最初的状态和最终状态即可解决它。 （Zhang Chaoyang使用轴的初始位置作为促进坐标的来源） 要建立物理模型，请选择适当的参数，假设杆M在初始时刻是源或源，或者将其用作土壤参考系统，并且杆M是水平的。传输坐标为x1。在绳索断裂之前，球M向轴M移动，杆M水平移动。因此，与源相关的球M的运动是一个组合的综合，这是两者的叠加。 CI与轴相关的球M的rcular运动可以是来自角度θ的参数和某种Gumove杆M的线性速度，即 在动量之后，球和轴的水平方向不受外部力的影响，因此保存了水平方向，并且两者的质量中心保持在水平方向上。为了鼓舞人心的叙述，我们仅考虑下面水平方向的中心。最初，由杆和球组成的系统中心是 其中，k = m/m。当绳索摧毁绳索时，系统的水平动量就会保存，质量中心保持不变。 由此，可以解决轴的X1的水平去除 （张·乔阳（Zhang Chaoyang 因此，可以通过取出Rod M的时间来获得速度。 然后找到球的V2速度。 V2OF的速度土地参考系统中的球相对于土地参考系统和球在杆M中的圆形运动速度相对于杆M的V1速度等于： 在我所在的地方，eθ是水平方向和切向的矢量单位，以及圆形运动。分别在水平和垂直方向的V2 因此 （Zhang Chaoyang计算速度平方与角度与绳索损坏时得出的时间之间的相关性） 根据能量护理，只有小球M在初始时刻具有动能，并且杆M始终固定在水平方向上。然后，最终状态是球的小能量动力学的总和，潜在的小球能量和杆M的动能的总和： 当θ= 37°时，绳索会破坏，球开始移动到抛物线运动。到ITO时，水平方向不受强大的影响，并以恒定速度以直线移动。垂直直接由于重力，n均匀地加速。 根据几何关系，可以看出，lcosθ从X1回到了小球M的位置。 点A是从点L的来源。降低球体坐标的水平位置，您可以在抛物线过程中确定水平去除： 垂直距离是 为了简化计算，请替换SIN37°= 0.6和COS37°= 0.8的值。从水平运动中，您会发现它。 替换在垂直方向上加速的同等运动以获得 （张·乔阳（Zhang Chaoyang）降低了抛物线运动的角度和时间之间的关系） 用能量护理产生的V0和θ之间的关系替换上述方程。 当您缺乏K时，您很明显，这与杆M质量相符，杆M几乎不稳定，V0返回第二个问题的结果。为了找到最低V0的数量，K试图判断T他单调性， 因此，如果V0随着K的升高而单调地变化，则更换k = 1的最小量，则可以获得最低初始速度量 2025年进入Heijiliao学院的问题 。 。一个磁场是-y0中注射的磁场，在（0，y0）中释放了磁场。 DE - 电颗粒仅受Lorentz力的影响，因此它们以圆形运动向磁场移动。根据几何关系，可以获得圆形运动的中心。 在循环运动的重新提交期间，洛伦兹力等于离心力。 （Zhan评论Chaoyang循环运动的几何关系） 由于入射角为30°，所以颗粒移至磁场的时间是整个周期的六分之一，并且完全圆形运动的t周期为 然后，磁场中带电颗粒的运动时间为 （2）第二个问题是负C哈格被放在Xoy平面上。带电的颗粒受到了洛伦兹力和伯爵力的影响，但是粒子运动的几何形状并未改变，并且圆形运动仍然存在。入射磁场的V2的初始速度已解决。洛伦兹力和县力都是力的中心力。为了确保在两个力的作用下颗粒仍在运动的圆形运动上移动，必须将负电荷放置在Lorentz力使NG圆形运动的圆的中间。否则，两者的中心是不平衡的，伯爵力量不可避免地会导致粒子偏离洛伦兹力引起的圆形运动，从而转向其他复杂行为。因此，根据牛顿的第二定律，有以下方程式 替换质量M的颗粒和半径R的圆形运动，我们可以获得第一次大约V2的二进制方程： 使用二进制方程IND根公式，我们将看到事件的速度是 由于V2速度不能为负，因此负数被抛弃，事件的最终速度为 （Zhang Chaoyang和根搜索公式的计算） （3）问题（3）和问题（2）是相同的条件。需要在磁性FI Exitseld的晶粒及其速度首次颠倒后解决T2时间。在检查物理过程时，当带电的颗粒沿圆形运动轨迹释放磁场时，洛伦兹力缺失，并且不可避免地圆形运动。目前，晶粒仅受到门廊力量的约束，方向总是指向负电荷的位置。为了使带电颗粒的速度颠倒，其运动轨迹应该是椭圆形的，当磁场简单释放时，将晶粒速度切入椭圆形轨迹。第一个速度是颠倒的是整个椭圆轨道运动的一半。这种情况与天堂系统非常相似，因此可以使用开普勒定律进行比较和解决。为了简化计算，让椭圆形R1和R2的围角座孔径分别为v1，当它出现时，速度为v2。 （张乔阳坚持认为带电颗粒的轨迹的运动是椭圆形） 检查开普勒的第二定律：该区域在时间单位内渗透了恒星和中央天体之间的连接是相同的。该法律本质上是保持角度的动力，也就是说 该区域在设备时通过恒星的身体以及椭圆轨道是 因此，椭圆轨道上的任何点符合 在整数时间内可以获得位置和天气之间的相关性是 （张乔阳评论开普勒的第二定律） 为了解决T和T2时期，需要解决椭圆形区域。面积椭圆形的面积可用于在形状 - 矩形坐标系统下使用椭圆方程。 通过这些要点，你可以 可以通过使用三角形交换元素或使用几何含义来实现进一步的整合，很明显，集成是解决圆形单元的面积。使用三角交换以获取元素 （张乔阳捕获了普通人的共同区域） 椭圆运动期之后 使用半肌轴A =（R1+R2）/2，半轴轴B和椭圆的半焦点长度C =（R2-R1）/2之间的关系，我们可以发现椭圆的半轴B 最后，使用能量预防和角度预防动量可以列出与V1和V2满意的方程式。 可以找到解决方案 替换V1，R1，M （Zhang Chaoyang共享R2/R1比率） 最后，以换取R1/R2，V1，A，B，然后获得 节目中的时间T2速度的第一个逆转是一半时期： 据了解，周日中午12点在SOHU视频中现场直播“张乔阳班”。网民可以搜索“ Zhang Chaoyang”来“遵循Sohu视频应用程序的流”，以观看实时广播和过去时代的完整视频重播；请按照“张Chaoyang”物理课程帐户查看“知识”点数简短的视频；此外，您还可以在SOHU新闻应用程序的“ SOHU技术”帐户中阅读每个物理课程的详细文章。回到Sohu看看更多